Сопротивление фильтра для акустики

Онлайн расчёт LC — фильтров 2-го порядка

Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC — фильтров, а также фильтров для акустических систем

LC — фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, причём наиболее древним из семейства фильтров, построенных при помощи индуктивностей и ёмкостей, является параллельный LC колебательный контур, изображённый на Рис.1.
Частотная зависимость коэффициента передачи такого LC контура соответствует характеристике резонансного полосового фильтра. Именно с этого самого простого LC-фильтра мы и начнём расчёт.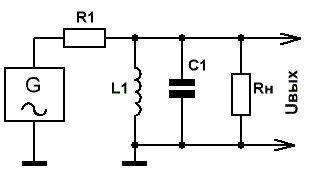

Как уже было сказано — LC контур, включённый по схеме, приведённой на Рис.1, представляет собой узкополосный полосовой резонансный фильтр, настроенный на частоту:
fо= 1/(2π√ LС ) .
На резонансной частоте сопротивление контура равно:
Rо = pQ , где р — это характеристическое сопротивление колебательного контура, численно равное: р = √ L/C , а
Q = fо/Δf — это параметр добротности LC контура, определяющий полосу пропускания фильтра по уровню 3 дБ.
Рис.1

А рассчитать добротность контура можно по формуле Q = p/R_пот = (√ L/C )/R_пот ,
где R_пот — это сумма сопротивлений потерь:
а) в катушке индуктивности (в первом приближении = активному сопротивлению катушки) и
б) в конденсаторе (сопротивление потерь в диэлектрике).

На низких частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше провод, тем проще его измерить активное сопротивление тестером.
На радиочастотах значение активного сопротивления катушки может составлять доли ома. Поэтому для расчёта добротности надо: либо найти сопротивление катушки в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L — длина в метрах, d — диаметр провода в мм. Либо (и лучше) — вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким внутренним сопротивлением, и определить добротность контура экспериментально.
Это решение является более правильным в связи с тем, что на высоких частотах на сопротивление потерь начинают влиять и другие факторы, в частности потери в конденсаторе, особенно если он окажется варикапом.

Нарисуем табличку с расчётом фильтра для низкочастотных приложений.

ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.

Если параметр активного сопротивления катушки R опущен, его значение принимается равным 100 Омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура. При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике десятки-сотни кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядки меньше характеристического сопротивления ρ.

Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.
Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как — потери в ферритах, наличие экрана, эффект близости витков и т. д. Поэтому вводить этот параметр в качестве входного я не стану — будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей частоты (Q=2πfL/R).
К тому же я добавлю сюда параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора — 1000, а для испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу ссылка на страницу .

ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.

Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).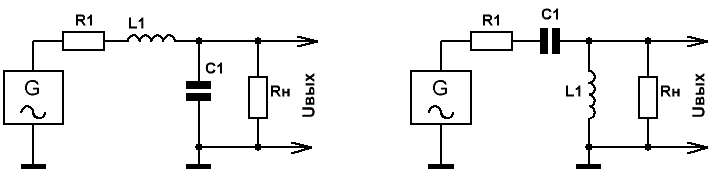

Рис.2

Источник

Проектирование и расчёт пассивных разделительных LC фильтров
(кроссоверов) для акустических систем

Онлайн калькулятор акустических фильтров 1. 6-го порядков: нижних частот (ФНЧ) для
низкочастотных динамиков, фильтров верхних частот (ФВЧ) – для высокочастотных,
а также полосовых фильтров (ПФ) – для среднечастотных.
Расчёт согласующей цепи Цобеля и Г- образного аттенюатора для громкоговорителя.

В настоящее время практически все качественные акустические системы являются многополосными, т. е. состоящими из нескольких громкоговорителей, каждый из которых работает в своём, отведённом ему диапазоне частот. Для распределения энергии звукового сигнала между динамиками используют электрические разделительные фильтры (КРОССОВЕРЫ), в данном рассматриваемом случае — пассивные LC-фильтры, которые включаются между выходным разъёмом усилителя, обладающего близким к нулю выходным сопротивлением, и динамической головкой АС.
Надо отметить, что данные разделительные фильтры являются одним из важнейших компонентов акустических систем, определяя весомую часть необходимых электроакустических характеристик, а также качества и естественности звучания тракта.

Сколько полос иметь? На каких частотах делить звуковой частотный диапазон? Какого типа и какого порядка использовать разделительные фильтры в кроссоверах, а также — какими эти фильтры будут обладать характеристиками — вот вопросы, которые устойчиво стоят на повестке дня и требуют аккуратного и подробного обсуждения.

Часть ответов на эти вопросы можно найти в довольно показательной таблице сравнительных характеристик различных фильтров, опубликованной в журнале «Автозвук», № 5/2001.
Таблица примечательна тем, что в ней приведены только реально применяемые кроссоверы без упоминания редко используемых типов фильтров, а также фильтров с нежелательными для акустики свойствами.

Краткая сравнительная характеристика разделительных фильтров акустических систем

Главным достоинством фильтров первого порядка является возможность одновременного достижения идеальной (плоской) АЧХ и идеальной (нулевой) ФЧХ. Недостаток фильтров первого порядка – слабые фильтрующие свойства

Любой фильтр второго, шестого, десятого и т.д. порядка обладает недостатком: при отсутствии переполюсовки динамиков АЧХ имеет провал, при переполюсовке возможны проблемы с импульсным откликом

Хороший фильтр с хорошим звуком. Отличные импульсные характеристики. Как правило, требует переполюсовки одной из головок

Обеспечивает гладкую АЧХ при очень хороших ФЧХ и импульсных характеристиках

Дает выброс 3 дБ на частоте раздела. Один из способов борьбы с выбросом – разнесение частот среза ФНЧ и ФВЧ

Фильтры третьего порядка обеспечивают достаточно высокую степень разделения при все ещё приемлемых ФЧХ и ГВЗ. Наиболее перспективны в большинстве устройств. Переполюсовка одной из головок приводит к иным последствиям, чем у фильтров 2-го порядка: АЧХ не меняется, характер ГВЗ улучшается, звук – дело вкуса

Имеет небольшое отклонение АЧХ от идеала в районе частоты раздела. Обладает улучшенными импульсными характеристиками

Применяется редко

Является основным среди фильтров третьего порядка, так как единственный обеспечивает плоскую АЧХ

Фильтры четвертого порядка применяются только в специальных случаях, когда по каким-то причинам требуется очень жесткое частотное разделение. ФЧХ и импульсные характеристики на грани допустимого. В отличие от фильтров второго порядка – не требуют переполюсовки

Практически не имеет отличий от фильтра Линквица – Райли

Обладает гладкой АЧХ

Используется редко

Используются чрезвычайно редко, например, при необходимости очень резкого ограничения полосы частот, подаваемых на низкочастотный динамик или сабвуфер. Переполюсовка просто вредна

Применяется редко

Применяется редко

Обладает гладкой АЧХ

Порядок фильтра	Бесселя	Линквица – Райли	Баттерворта
1
3
4
5

От себя добавлю, что действительно — фильтры 5-го порядка используются редко, однако если требуется существенное подавление внеполосных частот, подаваемых на сабвуфер, то в качестве ФНЧ, как правило, применяются фильтры не 5-го, а 6-го порядков и не Баттерворта, а Линквица – Райли.
Приведём схемы LC фильтров верхних и нижних частот 6-го порядка. Схемы фильтров меньших порядков образуются путём отбрасывания соответствующих элементов (Рис.1).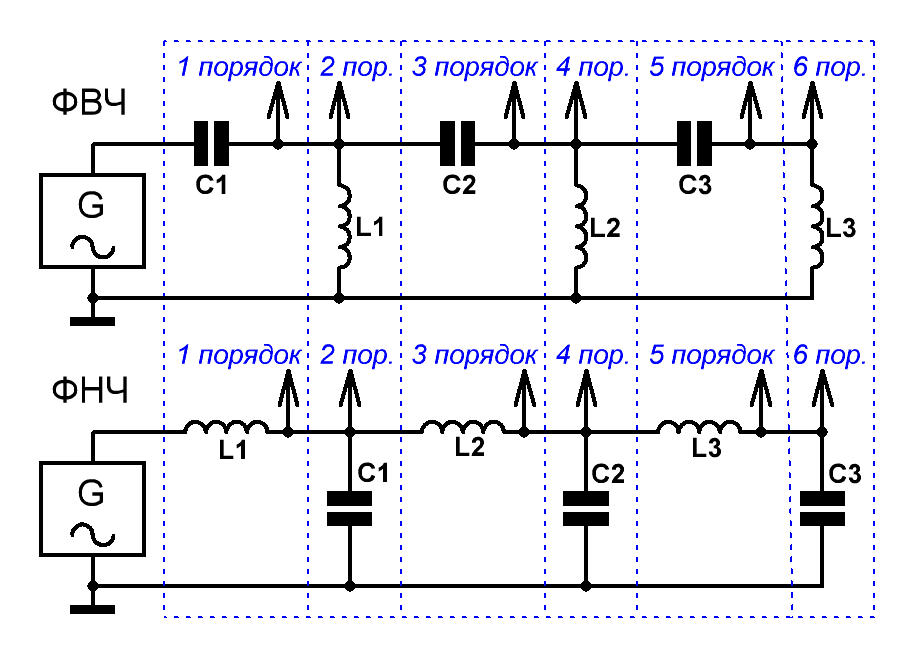

Рис.1 Схемы односторонне нагруженных LC фильтров верхних и нижних частот

Для фильтров нижних частот — значения величин элементов, соответствующих: порядку фильтра, сопротивлению нагрузки Rн и частоте среза (разделения) Fср, рассчитываются по следующим формулам:
L_i= α_i*R_н/(2πF_ср) ; C_i= α_i/(2πF_ср*R_н) , где α_i — это справочные нормированные значения (коэффициенты) для каждого элемента ФНЧ, называемые значениями элементов фильтра-прототипа.

Для фильтров верхних частот — каждая индуктивность из схемы ФНЧ заменяется ёмкостью, ёмкость — индуктивностью, которые, исходя из тех же самых коэффициентов, рассчитываются по формулам:
C_i= 1/(2πF_ср*α_i*R_н) ; L_i= R_н/(2πF_ср*α_i) .

Оставим все многочисленные таблицы со значениями нормированных коэффициентов фильтров-прототипов для справочной литературы, а сами сразу перейдём к онлайн расчёту номиналов элементов кроссоверов.

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ ФНЧ и ФВЧ LC- ФИЛЬТРОВ ДЛЯ АКУСТИЧЕСКИХ СИСТЕМ

Для полосовых фильтров: каждый элемент-индуктивность из НЧ фильтра-прототипа заменяется на последовательный LC контур (Рис.2), элементы которого рассчитываются по следующим формулам:
L_i= α_i*R_н/[2π(F_в — F_н)] , где Fн и Fв – нижняя и верхняя частоты среза полосового фильтра, а
C_i= 1/(4π 2 *F_н*F_в*L_i) .
Каждый элемент-ёмкость из фильтра-прототипа нижних частот заменяется на параллельный LC контур, элементы которого рассчитываются по формулам:
C_i= α_i/[2π*R_н*(F_в — F_н)] ;
L_i= 1/(4π 2 *F_н*F_в*C_i) .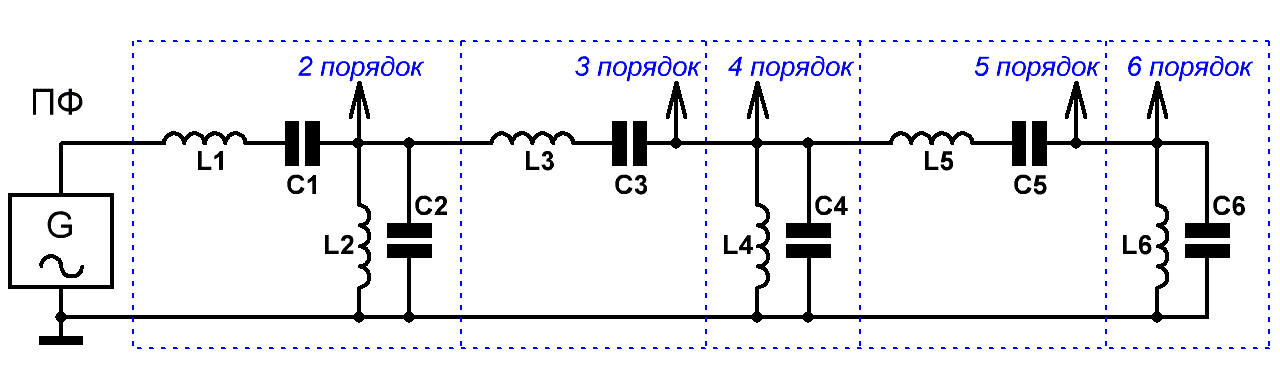

Рис.2 Схемы односторонне нагруженных LC полосовых фильтров

Разместим калькулятор расчёта элементов и для полосовых фильтров акустических систем.

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ ПОЛОСОВЫХ LC- ФИЛЬТРОВ ДЛЯ АКУСТИКИ

При расчёте разделительных фильтров принимается допущение, что нагрузка (сопротивление динамика) — это величина чисто активная. Однако, учитывая то, что реальные громкоговорители обладают комплексным характером входного сопротивления, то для корректной работы фильтров могут потребоваться согласующие цепи, компенсирующие этот комплексный характер.
При проектировании кроссоверов — частоты среза фильтров всегда следует выбирать значительно выше резонансных частот громкоговорителей. Тогда для компенсации комплексного характера входного сопротивления громкоговорителя будет достаточно включения упрощённой согласующей цепи, называемой цепью Цобеля и представляющей собой простую цепочку из последовательно включённых сопротивления Rк и ёмкости Cк (Рис.3а).
Рэй Олден, автор одной из самых популярных книг по акустике, советует использовать следующие соотношения: R_к = 1,25*R_е ; С_к = L_е/R_е 2 , где Re и Le — это паспортные сопротивление и индуктивность динамика.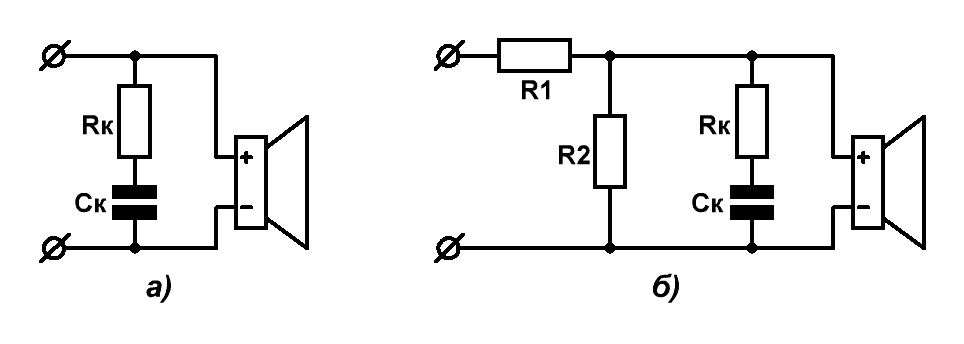

Рис.3 Согласующая цепь Цобеля и Г-образный аттенюатор для громкоговорителя

Также для уменьшения неравномерности суммарной АЧХ многополосной АС зачастую необходимо ослабить уровень каких-либо составляющих, как правило — среднечастотных либо высокочастотных. Это можно сделать с помощью Г-образных пассивных аттенюаторов, обеспечивающих заданный уровень ослабления N (дБ) (Рис.3б). Если задаться целью произвести ослабление без коррекции активного сопротивления громкоговорителя, то формулы для вычисления номиналов резисторов имеют следующий вид:
R1 ≈ R_e*(10 0,05N — 1)/10 0,05N ; R2 ≈ R_e/(10 0,05N — 1) .

Сдобрим пройденный материал калькуляторами.

КАЛЬКУЛЯТОР РАСЧЁТА ЦЕПИ ЦОБЕЛЯ ДЛЯ ГРОМКОГОВОРИТЕЛЯ

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ АТТЕНЮАТОРА ДЛЯ ГРОМКОГОВОРИТЕЛЯ

Следует отметить, что некоторые производители акустики игнорируют согласующие цепи, считая, что компенсация комплексной характеристики портит звучание системы на реальном музыкальном материале. В таких случаях неравномерность АЧХ тракта приходится устранять при помощи измерительной аппаратуры, кропотливо подбирая каждый из элементов звеньев фильтра.
В принципе — то же самое можно сделать и на симуляторе, подставив в качестве нагрузки фильтра эквивалентную электрическую схему громкоговорителя. Естественным образом — эта схема должна учитывать акустическое оформление динамика. А как создать такую схему — мы с вами подробно обсудили на странице ссылка на страницу.

Источник

Расчет пассивных разделительных фильтров в акустических системах

Данная статья поможет рассчитать электрические фильтры. Точность расчета высокая, но все же для точной подгонки АЧХ необходимо использовать микрофон, так как здесь АЧХ и импеданс условно считаются идеальными.

Разделительные фильтры с плоской АЧХ обладают рядом преимуществ перед фильтрами других типов, и являются наиболее употребляемыми в настоящее время в АС класса HI-FI. Поэтому в методике расчета будет рассмотрен только этот тип фильтров. Суть расчета состоит в том, что сначала разделительные фильтры рассчитываются из условия активной нагрузки и источника напряжения с бесконечно малым выходным сопротивлением (что справедливо для современных усилителей звуковой частоты). Затем принимаются меры, направленные на снижение влияния амплитудно-частотных и фазочастотных искажений громкоговорителей и комплексного характера их входного сопротивления на характеристики фильтров.

Расчет разделительных фильтров начинается с определения их порядка и нахождения параметров элементов лестничного фильтра прототипа нижних частот.

Фильтром-прототипом называется лестничный фильтр нижних частот, значения элементов которого нормированы относительно единичной частоты среза и единичной активной нагрузки. Рассчитав элементы фильтра нижних частот определенного порядка при реальной частоте и реальном значении сопротивления нагрузки, можно путем применения преобразования частоты определить схему и рассчитать значения элементов фильтра верхних частот и полосового фильтра соответствующего порядка. Нормированные значения элементов фильтра-прототипа, работающего от источника напряжения, определяются путем разложения в цепную дробь его выходной проводимости. Нормированные значения элементов фильтров-прототипов для расчета разделительных фильтров «всепропускающего типа с плоской АЧХ» 1…6-го порядка сведены в таблицу:

Порядок фильтра	Значение нормированных параметров значения z
	1	2	3	4	5	6
1	1,0	–	–	–	–	–
2	2,0	0,5	–	–	–	–
3	1,5	1,33	0,5	–	–	–
4	1,88	1,59	0,94	0,35	–	–
5	1,54	1,69	1,38	0,89	0,31	–
6	1,8	1,85	1,47	1,12	0,73	0,5

На рис.1 представлена схема фильтра-прототипа шестого порядка. Схемы фильтров прототипов меньших порядков образуются путем отбрасывания соответствующих элементов – α (начиная с больших) – например, фильтр-прототип 1-го порядка состоит из одной индуктивности α₁ и нагрузки R_н.

Рис. 1. Схема односторонне нагруженного фильтра-прототипа нижних частот 6-го порядка

Значение реальных параметров элементов, соответствующих выбранному порядку разделительных фильтров, сопротивлению нагрузки R_н (Ом) и частоте среза (разделения) f_d (Гц) рассчитываются следующим образом:

а) для фильтра нижних частот:

каждый элемент α-индуктивность фильтра-прототипа переводится в реальную индуктивность (Гн), рассчитываемую по формуле:

L=αR_н/2πf_d [1]

каждый элемент α-емкость фильтра-прототипа переводится в реальную емкость (Ф), рассчитываемую по формуле:

C=α/2πf_dR_н [2]

б) для фильтра верхних частот:

каждый элемент α-индуктивность фильтра-прототипа заменяется реальной емкостью рассчитываемой по формуле:

C=1/2πf_dαR_н [3]

каждый элемент α-емкость фильтра-прототипа заменяется реальной индуктивностью, рассчитываемой по формуле:

L=R_н/2πf_dα [4]

в) для полосового фильтра:

каждый элемент α-индуктивность заменяется на последовательный контур, состоящий из реальных L и C-элементов, рассчитываемых по формулам

L=αR_н/2π(f_d2-f_d1) [5]

где f_d2 и f_d1 – соответственно нижняя и верхняя частоты среза полосового фильтра,

где f₀=√ f_d1f_d2 – средняя частота полосового фильтра.

Каждый элемент α-емкость заменяется на параллельный контур, состоящий из реальных L и C-элементов, рассчитываемых по формулам:

С=α/2π(f_d2-f_d1)R_н, [7]

Пример. Требуется рассчитать значения элементов раздельных фильтров для трехполосной АС.

Выбираем разделительные фильтры второго порядка. Пусть выбранные значения частот разделения составляют: между низкочастотным и среднечастотным каналом f_d1=500 Гц, между среднечастотными и высокочастотными f_d2=5000 Гц. Сопротивление громкоговорителей на постоянном токе: низкочастотного и среднечастотного – 8 Ом, высокочастотного – 16 Ом.

Рис. 2. Пример расчета разделительных фильтров трехполосной АС а) АЧХ громкоговорителей без фильтров; б) АЧХ громкоговорителей с фильтрами, цепями согласования и коррекции; в) суммарная АЧХ АС на рабочей оси и при смещении микрофона на угол ±10° в вертикальной плоскости

Амплитудно-частотные характеристики громкоговорителей, измеренные в заглушенной камере на рабочей оси АС на расстоянии 1 м, изображены на рис.2, а) (низкочастотный громкоговоритель 100ГД-1, среднечастотный 30ГД-8, высокочастотный 10ГД-43).

Рассчитаем фильтр нижних частот:

Значение нормированных параметров элементов определим из таблицы: α₁=2,0, α₂=0,5.

Из рис.1 определяем схему фильтра-прототипа нижних частот: фильтр состоит из индуктивности α₁, емкости α₂ и нагрузки R_н.

Значения реальных элементов фильтров нижних частот находим по выражениям [1] и [2]:

L_{1 НЧ}=αR_н/2πf_d1=2,0·8,0/(2·3,14·500)=5,1 мГн,

C_{1 НЧ}=α/2πf_d1R_н=0,5/(2·3,14·500·8,0)=20 мкФ.

Значения элементов полосового фильтра (для среднечастотного громкоговорителя) определяем в соответствии с выражениями [5]…[8]:

L_{1 СЧ}=α₁R_н/2π(f_d2-f_d1)=2,0·8,0/2·3,14(5000-500)=0,566 мГн (сторона ВЧ)

С_{1 СЧ}=1/4π 2 f₀ 2 L_{1 СЧ}=1/4·3,14 2 ·5000·500·5,66·10 -4 =18 мкФ (сторона НЧ)

С_{2 СЧ}=α₂/2π(f_d2-f_d1)R_н=0,5/2·3,14(5000-500)·8,0=2,2 мкФ (сторона ВЧ)

L_{2 СЧ}=1/4π 2 f₀ 2 C_{2 СЧ}=1/4·3,14 2 ·5000·500·2,2·10 -6 =4,6 мГн (сторона НЧ)

Значения элементов фильтра верхних частот определяем в соответствии с выражениями [3] и [4]:

C_{1 ВЧ}=1/2πf_d2α₁R_н=1/(2·3,14·5000·2,0·16)=1,00 мкФ,

L_{2 ВЧ}=R_н/2πf_d2α₂=16/(2·3,14·5000·2,0)=0,25 мГн.

Для согласования фильтров с входным комплексным сопротивлением громкоговорителей может применяться специальная согласующая цепь. При отсутствии этой цепи входное сопротивление громкоговорителя оказывает влияние на АЧХ и ФЧХ разделительных фильтров. Параметры элементов согласующей цепи, включаемой параллельно громкоговорителю, находятся из условия:

Y_c(s)+Y_ГР(s)=1/R_E,

где Y_c(s) – проводимость согласующей цепи, Y_ГР(s) – входная проводимость громкоговорителя, R_E – электрическое сопротивление громкоговорителя на постоянном токе.

Схема согласующей цепи изображена на рис.3. Цепь является дуальной по отношению к эквивалентной электрической схеме громкоговорителя. Значения элементов цепи определяем следующим образом:

R_K1=R_E, [9]

C_K1=L_VC/R_E 2 [10]

L_K=C_MES R_E 2 =Q_ESR_E/2πf_s,

где L_VC – индуктивность звуковой катушки, f_s, C_MES, L_CES, R_ES – электромеханические параметры громкоговорителя.

Для компенсации входного сопротивления низкочастотного громкоговорителя применяют упрощенную цепь, состоящую из последовательно включенных сопротивления R_K1 и емкости C_K1. Это объясняется тем, что механический резонанс громкоговорителя не оказывает влияния на характеристики фильтра нижних частот и компенсируется только индуктивный характер входного сопротивления громкоговорителя. Целесообразность подключения полной согласующей цепи к высокочастотным и среднечастотным громкоговорителям оправдана в том случае, если резонансная частота громкоговорителя находится вблизи частоты среза фильтра верхних частот или нижней частоты среза полосового фильтра. В том случае, если частоты среза фильтров значительно выше резонансных частот громкоговорителей, включение упрощенной цепи является достаточным.

Рис.3. Схема согласующей цепи для компенсации комплексного характера входного сопротивления громкоговорителя

Влияние входного комплексного сопротивления громкоговорителей можно рассмотреть на примере разделительных фильтров второго порядка верхних и нижних частот [3] (рис.4).

Рис. 4. Электрическая эквивалентная схема громкоговорителя с разделительными фильтрами 2-го порядка: а – с фильтром нижних частот; б – с фильтром верхних частот; (1 – фильтр; 2 – громкоговоритель)

Параметры НЧ громкоговорителя выбраны таким образом, что его АЧХ соответствует аппроксимации по Баттерворту, т.е. полная добротность Q_ts=0,707. Частота среза фильтра нижних частот выбрана в 10 раз больше резонансной частоты громкоговорителя f_d=10f_s. Индуктивность звуковой катушки выбрана из условия: Q_VC=0,1, где Q_VC – добротность звуковой катушки, определяемая как:

Q_VC=L_VC2πf_s/R_E,

где f_s – резонансная частота громкоговорителя, R_E – сопротивление звуковой катушки на постоянном токе, L_VC – индуктивность звуковой катушки.

Значение Q_VC=0,1 соответствует среднестатистическому значению индуктивности звуковой катушки мощных низкочастотных громкоговорителей. Вследствие этого можно считать, что индуктивность звуковой катушки L_VC и активное сопротивление R_E включены параллельно емкости фильтра C₁ и образуют в области частоты среза фильтра широкий максимум АЧХ входного сопротивления, за которым следует острый провал (рис.5,а). Соответствующие изменения АЧХ фильтра по напряжению заключаются в небольшом подъеме АЧХ на частоте f≈2f_s (вследствие индуктивности звуковой катушки) и плавном провале, за которым следует резкий пик АЧХ из-за резонанса цепи, образуемой индуктивностью звуковой катушки и емкостью разделительного фильтра. Соответствующие изменения АЧХ и Z_BX после включения согласующей цепи из последовательно включенного резистора и конденсатора показаны на рис.5,а (кривые 2, 4, 6). Включение согласующей цепи приближает характер входного сопротивления громкоговорителя к активному и АЧХ разделительного фильтра по напряжению к желаемому. Однако вследствие влияния индуктивности звуковой катушки АЧХ по звуковому давлению отличается от желаемой (кривая 4), поэтому даже после согласующей цепи иногда требуется небольшая подстройка элементов фильтров и цепи согласования.

Рис. 5 АЧХ и входное сопротивление разделительных фильтров 2-го порядка, нагруженных на громкоговоритель: а) фильтр нижних частот; б) фильтр верхних частот;

1. АЧХ по напряжению на выходе фильтра без согласующей цепи;
2. АЧХ по напряжению на выходе фильтра с согласующей цепью;
3. АЧХ по звуковому давлению без согласующей цепи;
4. АЧХ по звуковому давлению с согласующей цепью;
5. входное сопротивление фильтра с громкоговорителем без согласующей цепи;
6. входное сопротивление фильтра с громкоговорителем с согласующей цепью.

В случае фильтра верхних частот влияние комплексного характера входного сопротивления громкоговорителя на входное сопротивление и АЧХ фильтра носит иной характер. Если частота среза фильтра верхних частот находится вблизи частоты резонанса громкоговорителя f_s (случай, иногда встречающийся в фильтрах для среднечастотных громкоговорителей, но практически невозможный для высокочастотных громкоговорителей), входное сопротивление фильтра верхних частот с громкоговорителем без согласующей цепи может иметь глубокий провал вследствие того, что на частоте резонанса громкоговорителя f_s его входное сопротивление значительно возрастает и имеет чисто активный характер. Фильтр оказывается как бы на холостом ходу, из-за резкого возрастания сопротивления нагрузки и его входное сопротивление определяется последовательно включенными элементами C₁, L₁. Чаще встречается ситуация, когда частота среза фильтра верхних частот f_d значительно выше частоты резонанса громкоговорителя f_s. На рис.5,б дан пример влияния входного сопротивления громкоговорителя и его компенсации на АЧХ фильтра верхних частот по напряжению и звуковому давлению. Частота среза фильтра выбрана значительно выше частоты резонанса громкоговорителя f_d≈8 f_s, параметры громкоговорителя Q_TS=1,5, Q_MS=10, Q_VC=0,08. Подъем АЧХ по звуковому давлению и напряжению в высокочастотной области, сопровождаемый провалом входного сопротивления, объясняется влиянием индуктивности звуковой катушки L_VC. На более высоких частотах АЧХ падает, а входное сопротивление растет за счет возрастания индуктивного сопротивления звуковой катушки.

Кривые 2, 4, 6 на рис.5,б показывают влияние согласующей RC-цепи.

Выходное сопротивление разделительного фильтра верхних частот, растущее с понижением частоты, оказывает влияние на электрическую добротность громкоговорителя, увеличивая ее, и соответственно увеличивает полную добротность и форму АЧХ по звуковому давлению. Иными словами, имеет место эффект «раздемпфирования» громкоговорителя. Для набежания этого необходимо выбирать крутизну спада АЧХ фильтра и частоту среза фильтра верхних частот f_d>>f_s так, чтобы на частоте резонанса f_s ослабление сигнала было не менее 20 дБ.

При расчете разделительных фильтров в примере, рассмотренном выше, принималось, что характер нагрузки – активный, поэтому рассчитаем согласующие цепи, компенсирующие комплексный характер входного сопротивления громкоговорителя.

Частота разделения низкочастотного и среднечастотного каналов f_d1 выбрана примерно на две октавы выше резонансной частоты среднечастотного громкоговорителя, а частота разделения среднечастотного и высокочастотного каналов f_d2 – на две октавы выше резонансной частоты высокочастотного громкоговорителя. Кроме того, можно принять, что индуктивность звуковой катушки высокочастотного громкоговорителя пренебрежимо мала в рабочем диапазоне частот и ей можно пренебречь (это справедливо для большинства высокочастотных громкоговорителей). В этом случае можно ограничиться применением упрощенной согласующей цепи для низкочастотного и среднечастотного громкоговорителей.

Пример . Измеренные (или определенные из кривой АЧХ входного сопротивления) индуктивности звуковых катушек: низкочастотного громкоговорителя L_VC=3·10 -3 Г=3 мГн, среднечастотного громкоговорителя L_VC=0,5·10 -3 Г=0,5 мГн. Тогда значение элементов компенсирующих цепей рассчитывают по формулам [9] и [10]:

для НЧ: R_K1–R_π=8 Ом; С_К1=L_VC/R 2 _E=3·10 -3 /64=47 мкФ

для СЧ: R’_K1=R_E-8 Ом; С’_К1=L_VC/R 2 _E=0,5·10 -3 /64=8,0 мкФ.

На АЧХ среднечастотного громкоговорителя имеется пик, увеличивающий неравномерность суммарной АЧХ АС (рис.2,а); в этом случае целесообразно включить амплитудный корректор. Режектирующее звено (рис.6) применяется для коррекции пиков АЧХ громкоговорителей или всей АС. Это звено имеет чисто активное входное сопротивление, равное сопротивлению нагрузки R_H и поэтому может быть включено между фильтром и громкоговорителем с скомпенсированным входным сопротивлением. В случае включения режектирующего звена на входе АС схема может быть упрощена, так как отпадает необходимость в элементах C_q, L_q, R_q, обеспечивающих активный характер входного сопротивления звена. Значения элементов рассчитываются по формулам:

R_K≈R_H(10 -0,05 N -1),

L_K=R_K∆f/2πf₀ 2 ,

C_K=1/L_K4π 2 f₀ 2 ,

C_q=L_K/R_H 2 ,

L_q=C_KR_H 2 ,

R_q=R_H(1+ R_H/R_K),

где R_H – сопротивление громкоговорителя (скомпенсированное) или входное сопротивление АС (Ом) в области резонансной частоты режектирующего звена;

∆f – полоса частот корректируемого пика АЧХ (отсчитывается по уровню – 3 дБ), Гц;

f₀ – резонансная частота режектора, Гц;

N – величина пика АЧХ, дБ.

Рис. 6. Режектирующее звено: а) принципиальная схема; б) АЧХ

Применим режектирующее звено, включенное между фильтром и среднечастотным громкоговорителем с согласующей цепью.

Из АЧХ среднечастотного громкоговорителя определяем ∆f=1850 Гц, f₀=4000 Гц, N=6 дБ. Сопротивление среднечастотного громкоговорителя с согласующей цепью R_H=8 Ом.

Значения элементов режектирующего звена следующее:

R_K≈R_H(10 -0,05 N -1)=8(10 -0,05·6 -1)=7,96 Ом,

L_K=R_K∆f/2πf₀ 2 =7,96·1850/2π(4000) 2 =0,147 мГн,

C_K=1/L_K4π 2 f₀ 2 =1/1,47·10 -4 (2π4000) 2 =11мкФ,

C_q=L_K/R_H 2 =1,47·10 -4 /64=2,3 мкФ,

L_q=C_KR_H 2 =10,8·10 -6 ·64=0,7 мГн,

R_q=R_H(1+ R_H/R_K)=8(1+8/7,96)≈16,0 Ом.

В рассматриваемом примере АЧХ высокочастотного и среднечастотного громкоговорителя имеют средние уровни примерно на 6 дБ и соответственно 3 дБ выше, чем АЧХ низкочастотного громкоговорителя (запись звукового давления осуществлялась при подаче на все громкоговорители синусоидального напряжения одинаковой величины). В этом случае для уменьшения неравномерности суммарной АЧХ АС необходимо ослабить уровень среднечастотных и высокочастотных составляющих. Это можно сделать либо с помощью корректирующего высокочастотного звена первого порядка (рис.7), элементы которого рассчитываются по формулам:

R_K≈R_H(10 -0,05 N -1),

L_K=R_K/2πf_d√(10 0,1 N -2), N≥3 дБ,

Либо с помощью Г-образных пассивных аттенюаторов, обеспечивающих заданный уровень ослабления N (дБ) и заданное входное сопротивление R_BX (рис.8). Значение элементов аттенюатора рассчитываем по формулам:

R₁≈R_BX(1-10 -0,05 N ),

R₂≈R_HR_BX10 -0,05 N /(R_H–R_BX10 -0,05 N ).

Рис. 7. Звено 1-го порядка, корректирующее высокие частоты: а) принципиальная схема; б) АЧХ

Рис. 8. Пассивный Г-образный аттенюатор

Рассчитаем для примера значения элементов аттенюатора для ослабления на 6 дБ сигнала высокочастотного громкоговорителя. Пусть входное сопротивление громкоговорителя с включенным аттенюатором равняется входному сопротивлению громкоговорителя, т.е. 16 Ом, тогда:

R₁≈16(1-10 -0,05·6 )≈8,0 Ом, R₂≈16·10 -0,05·6 /(1-10 -0,05·6 )≈16,0 Ом.

Аналогично рассчитаем значения элементов аттенюатора для среднечастотного громкоговорителя: R₁=4,7 Ом, R₂=39 Ом. Аттенюаторы включаются сразу после громкоговорителей с согласующими цепями.

Полная схема разделительных фильтров изображена на рис.9, АЧХ АС с рассчитанными фильтрами – на рис.2,в.

Как было сказано выше, фильтры четных порядков допускают только один вариант полярности включения громкоговорителей, в частности, фильтры второго порядка требуют включения в противофазе. Для рассматриваемого примера низкочастотный и высокочастотный громкоговоритель должны иметь идентичную полярность включения, а среднечастотный – обратную. Требования к полярности включения громкоговорителей рассматривались выше на модели АС с идеальными громкоговорителями. Поэтому при включении реальных громкоговорителей, имеющих собственную ФЧХ≠0, (в случае выбора частот разделения вблизи граничных частот рабочего диапазона громкоговорителей или при большой неравномерности АЧХ громкоговорителей) условие согласования реальных ФЧХ каналов может не соблюдаться. Поэтому для контроля реальной ФЧХ по звуковому давлению громкоговорителей с фильтрами необходимо пользоваться фазометром с линией задержки или определять условие согласования косвенно по характеру суммарной АЧХ АС в полосах разделения каналов. Правильной полярностью включения громкоговорителей можно считать ту, которая соответствует меньшей неравномерности суммарной АЧХ в полосе разделения каналов. Точное согласование ФЧХ разделяемых каналов при удовлетворении всем остальным требованиям (плоская АЧХ и т.д.) осуществляется численными методами синтеза оптимальных разделительных фильтров-корректоров на компьютере.

Рис.9. Принципиальная электрическая схема АС с рассчитанными разделительными фильтрами (емкости в микрофарадах, индуктивности – в миллигенри, сопротивления – в омах).

В разработке пассивных разделительных фильтров важную роль играет их конструкция, а также выбор типа конкретных элементов – конденсаторов, катушек индуктивности, резисторов, в частности, большое влияние на характеристики АС с фильтрами оказывает взаимное размещение катушек индуктивности, при их неудачном расположении вследствие взаимной связи возможны наводки сигнала между близко расположенными катушками. По этой причине их рекомендуется располагать взаимно перпендикулярно, только такое расположение позволяет свести к минимуму их влияние друг на друга. Катушки индуктивности являются одним из важнейших компонентов пассивных разделительных фильтров. В настоящее время многие зарубежные фирмы применяют катушки индуктивности на сердечниках из магнитных материалов, обеспечивающих большой динамический диапазон, низкий уровень нелинейных искажений и малые габариты катушек. Однако конструирование катушек с магнитными сердечниками связано с применением специальных материалов, поэтому до настоящего времени многие разработчики применяют катушки с воздушными сердечниками, основные недостатки которых – большие габариты при условии малых потерь (особенно в фильтре низкочастотного канала), а также большой расход меди; достоинства – пренебрежимо малые нелинейные искажения.

Конфигурация катушки индуктивности с воздушным сердечником, изображенная на рис.10, является оптимальной, так как она обеспечивает максимальное отношение L/R, т.е. катушка с заданной индуктивностью L, намотанная проводом выбранного диаметра, имеет при данной конфигурации намотки наименьшее сопротивление R или наибольшую добротность по сравнению с любой другой. Отношение L/R, имеющее размерность времени, связано с размерами катушки соотношением [3.13]:

L – в микрогенри, R – в омах, a, l, c – в миллиметрах.

Рис.10. Катушка индуктивности с воздушным сердечником оптимальной конфигурации: а) в разрезе; б) внешний вид.

Расчетные соотношения для данной конфигурации катушки: a=1,5с, l=c; конструктивный параметр катушки c=√(L/R8,66), число витков N=19,88√(L/c), диаметр провода в миллиметрах, d=0,841c/√N, масса провода (материал – медь) в граммах, q=c 3 /21, длина провода в миллиметрах, B=187,3√Lc. В том случае, если катушка индуктивности рассчитывается, исходя из провода данного диаметра, основные расчетные соотношения выглядят следующим образом:

конструктивный параметр c= 5 √(d 4 19,88 2 L/0,841 4 )=3,8 5 √(d 4 L), сопротивление провода R=L/c 2 8,66.

Найдем, для примера параметры катушки индуктивности рассчитанного ранее фильтра нижних частот. Индуктивность катушки составляет L_1НЧ=5,1 мГ. Сопротивление R катушки на постоянном токе определим из допустимого затухания сигнала, вносимого реальной катушкой на низких частотах. Пусть ослабление сигнала за счет потерь R в катушке составляет N≤1дБ. Поскольку сопротивление низкочастотного громкоговорителя на постоянном токе составляет R_E=8 Ом, то допустимое сопротивление катушки, определяемое из выражения R≤R_E(10 0,05N -1), составляет R≤0,980 Ом; тогда конструктивный параметр катушки c=√5100/0,98·8,66=24,5 мм; количество витков N=19,8√(5100/24,5)=287 витков; диаметр провода d=0,841·24,5/√287=1,2 мм; масса провода q=24,5 3 /21,4≈697 г; длина провода B=187,3√(85,1·24,5)≈46 м.

Другим важным элементом пассивных разделительных фильтров являются конденсаторы. Обычно в фильтрах используют бумажные или пленочные конденсаторы. Из бумажных наиболее употребляемые отечественные конденсаторы МБГО. Достоинством этих типов конденсаторов являются малые потери, высокая температурная стабильность, недостатком – большие габариты, снижение допустимого максимального напряжения на высоких частотах. В настоящее время в фильтрах ряда зарубежных АС используют электролитические неполярные конденсаторы с малыми внутренними потерями, объединяющие достоинства рассмотренных конденсаторов и свободные от их недостатков.

По материалам из книги: «Высококачественные акустические системы и излучатели»

(Алдошина И.А., Войшвилло А.Г.)

Источник