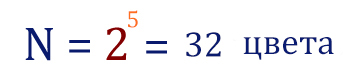7 задание егэ информатика стерео

Задание 7. Кодирование и декодирование информации

За правильное выполненное задание получишь 1 балл. На решение отводится примерно 5 минут.

Для выполнения задания 7 по информатике необходимо знать:

• I — объем информации
• для хранения растрового изображения нужно выделить в памяти I= N · i битов, где N – количество пикселей и i – глубина цвета (разрядность кодирования)
• количество пикселей изображения N вычисляется как произведение ширины рисунка на высоту (в пикселях)
• глубина кодирования – это количество бит, которые выделяются на хранение цвета одного пикселя
• объём музыкального файла вычисляется по формуле I = f*r*k*t, где f – частота дискретизации, r – разрешение (глубина кодирования), k – количество каналов, t – время звучания
• пропускная способность канал B = f*r*k

Задачи для тренировки

Автоматическая фотокамера производит растровые изображения размером 640×480 пикселей. При этом объём файла с изображением не может превышать 320 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?

Для хранения произвольного растрового изображения размером 256×1024 пикселей отведено 64 Кбайт памяти, при этом для каждого пикселя хранится двоичное число – код цвета этого пикселя. Для каждого пикселя для хранения кода выделено одинаковое количество бит. Сжатие данных не производится. Какое максимальное количество цветов можно использовать в изображении?

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512 на 128 пикселов при условии, что в изображении могут использоваться 512 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Музыкальный фрагмент был записан в формате стерео (двухканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 100 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 3 раза выше и частотой дискретизации в 5 раз меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Музыкальный фрагмент был записан в формате моно, оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла – 98 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате стерео (двухканальная запись) и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 3,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи.

Источник

ЕГЭ по информатике 2022 — Задание 7 (Фото, звук)

Седьмое задание из ЕГЭ по информатике 2022. Отличное задание, которое нужно решать!

Данное задание проверяет умение определять объём памяти, необходимый для хранения графической и звуковой информации.

Приступим к примерным вариантам из ЕГЭ по информатике.

Задача (классика, количество цветов изображения)

Какое максимальное количество цветов может быть в палитре неупакованного растрового изображения, имеющего размер 1024 * 256 пикселей и занимающего на диске не более 165 кб.

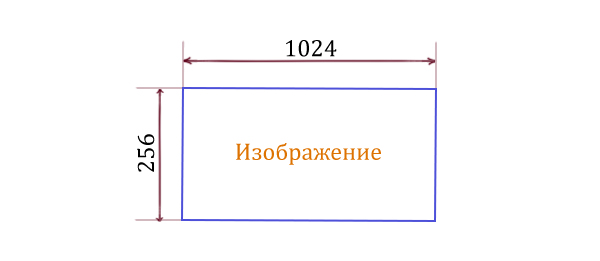
1. Найдём сколько будет весить один пиксель! У нас всего 1024 * 256 пикселей. Берём максимально возможный объём картинки (165 Кб) и разделим его на количество пикселей.

Важно: Мы не пытаемся сразу вычислить, например, количество пикселей во всём изображении. А записываем сначала в виде действия 1024 * 256. Когда уже получается дробь, пытаемся сократить эту дробь по максимуму. Это позволяет экономить силы при решении седьмого задания из ЕГЭ по информатике 2022.

Нам нужно найти: сколько именно целых бит занимает один пиксель. Округляем количество бит в меньшую сторону, потому что мы не можем «перевалить» за максимальную отметку 165 Кб для всего изображения.

Применим формулу, которую нужно твёрдо знать для решения 7 задания из ЕГЭ по информатике.

Задача (Резервирование памяти)

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64 * 256 пикселей при условии, что в изображении могут использоваться 4 различных цвета? В ответе запишите только целое число, единицу измерения писать не нужно.

Задача обратная предыдущей. Первый вопрос на который нужно ответить: сколько весит 1 пиксель? Снова используется формула N = 2 i .

Видно, что 1 пиксель имеет объём i = 2 бита. Количество пикселей в изображении равно 64 * 256. Важно опять умножать эти два числа не сразу. Тогда объём картинки будет равен: количество пикселей (64 * 256) умножить на объём одного пикселя (2 бита).

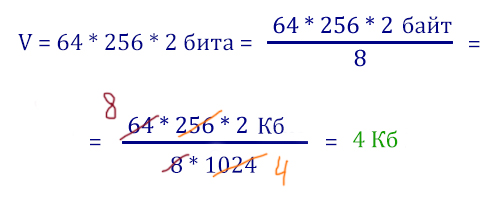
В подобных задачах из ЕГЭ по информатике фишка в том, чтобы составить дробь и потом сократить её, тем самым вычисление делается без калькулятора и без лишних усилий.

Производится звукозапись музыкального фрагмента в формате квадро (четырёхканальная запись) с частотой дискретизации 16 кГц и 24-битным разрешением. Результаты записываются в файл, сжатие данных не производится; размер полученного файла 60 Мбайт. Затем производится повторная запись этого же фрагмента в формате стерео (двухканальная запись) с частотой дискретизации 64 кГц и 16-битным разрешением. Сжатие данных не производилось. Укажите размер файла в Мбайт, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно.

Общая формула для решения 7-ого задания на тему звуковых файлов из ЕГЭ по информатике.

Её легко запомнить. Объём записанного файла равен произведению всех остальных параметров. Важно соблюдать единицы измерения.

Распишем формулу дискретизации для первой звукозаписи и для второй. В первом случае у нас режим квадро, значит, нужно к произведению добавить ещё 4. Во втором случае режим стерео, значит, должны поставить коэффициент 2. Т.к. производилась запись этого же фрагмента, то время в обоях случаях одинаковое.

Выражаем время из первого уравнения и подставляем во второе.

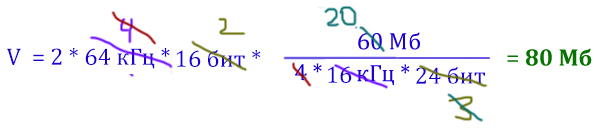
Опять удобно решать с помощью сокращение дробей.

Закрепим результат, решив ещё одну тренировочную задачу из ЕГЭ по информатике 2021.

Задача (ЕГЭ по информатике 2020, Досрочная волна)

Музыкальный фрагмент был записан в формате квадро (четырёхканальная запись), оцифрован и сохранён в виде файла без использования сжатия данных. Размер полученного файла без учёта размера заголовка файла – 12 Мбайт. Затем тот же музыкальный фрагмент был записан повторно в формате моно и оцифрован с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Укажите размер в Мбайт файла, полученного при повторной записи. В ответе запишите только целое число, единицу измерения писать не нужно. Искомый объём не учитывает размера заголовка файла.

Вначале выписываем формулу для первого файла и для второго файла. Подставляем всё, что нам известно.

Для второго звукового файла коэффициенты все переносим в одну сторону.

Выражаем из первого уравнения произведение M * i * t и подставляем его во второе уравнение.

После небольших сокращений получаем 4 Мб для второго звукового файла.

Время было для обоих файлов одинаковым, потому что было сказано, что тот же музыкальный файл перезаписали второй раз с другими параметрами.

Удачи при решении 7 задания из ЕГЭ по информатике 2022!

Источник

7 задание егэ информатика стерео

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 24-битным разрешением. В результате был получен файл размером 48 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число.

Так как частота дискретизации 64 кГц, то за одну секунду запоминается 64000 значений сигнала.

Глубина кодирования 24 бита, т. е. 3 байта. Т. к. запись двухканальная, объём памяти, необходимый для хранения данных одного канала, умножается на 2, поэтому, так как потребовалось 48 Мбайт, один канал занимает 24 Мбайт или 24·2 20 байт. Чтобы найти время, в течение которого проводилась запись, необходимо разделить найденный информационный объем на глубину кодирования и на частоту дискретизации:

Тем самым, время записи примерно равно 2 минутам.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 48 кГц и 24-битным разрешением. В результате был получен файл размером 5625 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) производилась запись. В качестве ответа укажите ближайшее к времени записи целое число, кратное 5.

Так как частота дискретизации 48 кГц, то за одну секунду запоминается 48 000 значений сигнала. Т. к. запись двухканальная, объём памяти, необходимый для хранения данных одного канала, умножается на 2

Разрешение — 24 бита = 3 байта, размер файла 5625 Мб = 5625·1 048 576 байт. Время записи определится следующим образом: t = 5625 · 1 048 576 / (48 000 · 3 · 2) = 20480 секунд ≈&nbsp341 минута. В ответе требуется указать ближайшее к времени записи число, кратное 5, то есть 340 минут.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 24-битным разрешением. В результате был получен файл размером 72 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число.

Так как частота дискретизации 64 кГц, то за одну секунду запоминается 64000 значений сигнала.

Глубина кодирования 24 бита, т. е. 3 байта. Т. к. запись двухканальная, объём памяти, необходимый для хранения данных одного канала, умножается на 2. Поскольку потребовалось 72 Мбайтa, один канал занимает 36 Мбайт или 36·2 20 байт. Чтобы найти время, в течение которого проводилась запись, необходимо разделить найденный информационный объем на глубину кодирования и на частоту дискретизации:

Тем самым, время записи примерно равно 3 минутам.

Производилась двухканальная (стерео) звукозапись с частотой дискретизации 64 кГц и 16-битным разрешением. В результате был получен файл размером 32 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько времени (в минутах) проводилась запись. В качестве ответа укажите ближайшее к времени записи целое число.

Так как частота дискретизации 64 кГц, то за одну секунду запоминается 64000 значений сигнала.

Глубина кодирования 16 бит, т. е. 2 байта. Т. к. запись двухканальная, объём памяти, необходимый для хранения данных одного канала, умножается на 2. Поскольку потребовалось 32 Мбайтa, один канал занимает 16 Мбайт или 16·2 20 байт. Чтобы найти время, в течение которого проводилась запись, необходимо разделить найденный информационный объем на глубину кодирования и на частоту дискретизации:

Тем самым, время записи примерно равно 2 минутам.

131 секунд примерно больше чем 2 минуты, поэтому количество минут надо округлять до 3 минут, 2 минут не хватит по любому!

131с. ближе к 120, чем к 180, поэтому округление проводится в меньшую сторону.

Производилась четырехканальная (квадро) звукозапись с частотой дискретизации 24 кГц и 16-битным разрешением. В результате был получен файл размером 1800 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько минут производилась запись.

В качестве ответа укажите ближайшее к времени записи целое число минут.

Так как частота дискретизации 24 кГц, то за одну секунду запоминается 24000 значений сигнала.

Глубина кодирования 16 бита, т. е. 2 байта. Т. к. запись четырёхканальная, объём памяти, необходимый для хранения данных одного канала, умножается на 4, поэтому, так как потребовалось 1800 Мбайт, один канал занимает 450 Мбайт или 450·2 20 байт. Чтобы найти время, в течение которого проводилась запись, необходимо разделить найденный информационный объем на глубину кодирования и на частоту дискретизации:

сек.

Тем самым, время записи примерно равно 163,84 минуты, что близко к 164 минутам.

Источник

Старое Разбор 7 задания ЕГЭ по информатике

Объяснение заданий 7 ЕГЭ по информатике

Типы ссылок в ячейках

Формулы, записанные в ячейках таблицы, бывают относительными, абсолютными и смешанными.

Имена ячеек в относительной формуле автоматически меняются при переносе или копировании ячейки с формулой в другое место таблицы:

Относительная адресация:
имя столбца вправо на 1
номер строки вниз на 1

Абсолютная адресация:
имена столбцов и строк при копировании формулы остаются неизменными

Стандартные функции Excel

В ЕГЭ встречаются в формулах следующие стандартные функции:

• СЧЕТ — количество непустых ячеек,
• СУММ — сумма,
• СРЗНАЧ — среднее значение,
• МИН — минимальное значение,
• МАКС — максимальное значение

В качестве параметра функции везде указывается диапазон ячеек: МИН(А2:А240)

следует иметь в виду, что при использовании функции СРЗНАЧ не учитываются пустые ячейки и текстовые ячейки; например, после ввода формулы в C2 появится значение 2 (не учитывается пустая А2):

Построение диаграмм

• Диаграммы используются для наглядного представления табличных данных.
• Разные типы диаграмм используются в зависимости от необходимого эффекта визуализации.
• Так, круговаяи кольцеваядиаграммы отображают соотношение находящихся в выбранном диапазоне ячеек данных к их общей сумме. Иными словами, эти типы служат для представления доли отдельных составляющих в общей сумме.
• Соответствие секторов круговой диаграммы (если она намеренно НЕ перевернута) начинается с «севера»: верхний сектор соответствует первой ячейке диапазона.

Типы диаграмм Линейчатаяи Гистограмма(на левом рис.), а также Графики Точечная(на рис. справа) отображают абсолютные значения в выбранном диапазоне ячеек.

Решение заданий ЕГЭ по информатике

Рассмотрим, как решается задание 7 ЕГЭ по информатике.

Анализ диаграмм

На диаграмме отображено количество участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение общего количества участников (из всех трех регионов) по каждому из предметов тестирования?

✍ Решение:

• столбчатая диаграмма позволяет определить числовые значения. Так, например, в Татарстане по биологии количество участников 400 и т.п. Найдем с помощью нее общее количество участников со всех регионов по каждому предмету. Для этого посчитаем значения абсолютно всех столбцов в диаграмме:
• по круговой диаграмме можно определить только доли отдельных составляющих в общей сумме: в нашем случае это доли участников по различным предметам тестирования;
• для того чтобы разобраться, какая круговая диаграмма подходит, сначала посчитаем самостоятельно долю участников, тестирующихся по отдельным предметам; для этого из столбчатой диаграммы вычислим сумму участников по каждому предмету и разделим на уже полученное в первом пункте общее количество участников:
• Теперь сравним полученные данные с круговыми диаграммами. Данные соответствуют диаграмме под номером 1 .

Результат: 1

Предлагаем посмотреть подробный разбор данного 7 задания на видео:

На диаграмме отображено количество участников тестирования по предметам в разных регионах России.

Какая из диаграмм правильно отражает соотношение количества участников тестирования по истории в регионах?

✍ Решение:

Подробный разбор задания смотрите на видео:

Копирование формул

Дан фрагмент электронной таблицы.

Из ячейки A3 в ячейку С2 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились.
Каким стало числовое значение формулы в ячейке С2?

✍ Решение:

Результат: 180

Разбор данного 7 задания смотрите на видео:

Дан фрагмент электронной таблицы. Из ячейки A3 в ячейку E2 была скопирована формула. При копировании адреса ячеек автоматически изменились.
Каким стало числовое значение формулы в ячейке E2?

✍ Решение:

• Рассмотрим формулу в ячейке A3: = $E$1*A2 . Знак доллара означает абсолютную адресацию: при копировании формулы буква или цифра, стоящая рядом с долларом, не изменится. То есть в нашем случае сомножитель $E$1 так и останется в формуле при копировании.
• Поскольку копирование осуществляется в ячейку E2, необходимо посчитать на сколько столбцов вправо переместится формула: на 5 столбцов (от A до E). Соответственно, и в сомножителе A2 буква A заменится на E.
• Теперь посчитаем на сколько строк вверх сместится при копировании формула: на одну (c A3 на E2). Соответственно и в сомножителе A2 цифра 2 заменится на 1.
• Получим формулу и посчитаем результат: =$E$1*E1 = 1

Результат: 1

Дан фрагмент электронной таблицы. Из ячейки B3 в ячейку A4 была скопирована формула. При копировании адреса ячеек в формуле автоматически изменились.
Каким стало числовое значение формулы в ячейке A4?

Примечание: знак $ обозначает абсолютную адресацию.

✍ Решение задания 7:

• Знак доллара $ означает абсолютную адресацию:
• $ перед буквой означает фиксацию столбца: т.е. при копировании формулы название столбца меняться не будет;
• $ перед цифрой означает фиксацию строки: при копировании формулы название строки меняться не будет.
• В нашем случае меняться не будут выделенные буквы и цифры: = $C 2 + D $3
• Копирование же формулы на один столбец влево, означает, что буква D (в D$3) должна поменяться на предшествующую ей C. При копировании формулы вниз на одну строку, значение 2 (в $C2) меняется на 3.
• Получаем формулу:
• В итоге имеем результат: 300 + 300 = 600

Результат: 600

Подробное решение данного 7 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

Какая формула была записана

Коле нужно с помощью электронных таблиц построить таблицу значений формулы 5х–3у для значений х и у от 2 до 5. Для этого сначала в диапазонах В1:Е1 и А2:А5 он записал числа от 2 до 5. Затем в ячейку В2 записал формулу (А2 – значение х; В1 – значение у), после чего скопировал её во все ячейки диапазона B2:E5. В итоге получил таблицу, представленную ниже.

Какая формула была записана в ячейке В2?

Примечание: знак $ используется для обозначения абсолютной адресации.

✍ Решение:

• Мысленно представим копирование ячейки с формулой отдельно по горизонтали и по вертикали.

В формуле ссылка на столбец А не должна менять букву при копировании, значит, перед ней необходимо поставить знак $ :

Тогда как имя столбца B должно меняться (на C, D, E), чтобы цифры в вычитаемом менялись (3, 4, 5):

По вертикали:

Номер строки в уменьшаемом должен меняться, чтобы цифры в нем увеличивались (3, 4, 5). Тогда как строки в вычитаемом меняться не должны: $A2. Таким образом, необходимо поставить знак $ перед номером строки в уменьшаемом: B$1

В результате получаем формулу: = 5 * $A2 – 3 * B$1 , что соответствует номеру 2 .

Результат: 2

Значение формулы СУММ или СРЗНАЧ

Задан фрагмент электронной таблицы:

Как изменится значение ячейки C3, если после ввода формул переместить содержимое ячейки B2 в B3?
(«+1» означает увеличение на 1, «-1» означает уменьшение на 1):

✍ Решение:

Проанализируем данные электронной таблицы до перемещения:

В ячейке C2 будет находиться число 4, так как функция СЧЁТ подсчитывает количество непустых ячеек указанного диапазона.

В ячейке С3 будет находиться число 3:

Теперь посмотрим, что произойдет после перемещения:

Перемещение содержимого ячейки означает, что ячейка B2 окажется пустой, а в ячейке B3 появится число 6.

Тогда расчёт формулы в ячейке C2 поменяется: количество непустых ячеек диапазона A1:B2 станет равным 3.

Соответственно изменится и значение после расчёта формулы ячейки C3: среднее значение содержимого диапазона ячеек A1:C2 станет равным:

(нужно не забывать, что функция СРЗНАЧ не учитывает пустые ячейки, поэтому ячейка B2 не учтена).

Таким образом, значение после перемещения формулы изменилось, уменьшившись на 1. Верный ответ 2

Результат: 2

Подробное решение задания на видео:

В электронной таблице значение формулы =СРЗНАЧ(С2:С5) равно 3.

Чему равно значение формулы =СУММ(С2:С4) , если значение ячейки С5 равно 5?

✍ Решение:

• Функция СРЗНАЧ предназначена для вычисления среднего арифметического значения указанного диапазона ячеек. Т.е. в нашем случае среднее значение ячеек C2, C3, C4, C5.
• Результат функции =СРЗНАЧ(С2:С5) задан по условию, подставим его в формулу:
• Примем неизвестную сумму в за x и получим по формуле вычисления среднего значения:
• Найдем x:
• По заданию необходимо найти =СУММ(С2:С4) . Зная значение в ячейке С5, вычтем его из полученной суммы и найдем ответ:

Результат: 7

Подробное решение смотрите на видео:

Какое число должно быть записано в ячейке

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке А1, чтобы диаграмма, построенная по значениям ячеек А2:С2, соответствовала рисунку? Известно, что все значения ячеек из рассматриваемого диапазона неотрицательны.

✍ Решение:

• Имеем круговую диаграмму, которая отображает доли отдельных составляющих в общей сумме. По изображению диаграммы можно судить о том, что, скорее всего, значения во всех ячейках формулы должны быть равны (секторы диаграммы визуально равны).
• Получим выражения из формул ячеек, подставив вместо A1 ->x:
• Так как секторы диаграммы равны, то приравняем любые два из полученных выражений (например, С2 = А2):
• По условию задания число не должно быть отрицательным, поэтому нам подходит 5

Результат: 5

Для более детального разбора предлагаем посмотреть видео решения данного 7 задания ЕГЭ по информатике:

Рассмотрим еще один пример решения 7 задания ЕГЭ по информатике:

Дан фрагмент электронной таблицы:

Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек А2:С2 соответствовала рисунку?
Известно, что все значения диапазона, по которым построена диаграмма, имеют один и тот же знак.

✍ Решение:

• Круговая диаграмма отображает доли отдельных частей в общей сумме. В нашем случае в диаграмме отражаются результаты вычисления формул в ячейках А2:С2
• По диаграмме можно судить о том, что, скорее всего, полученные значения в формулах во всех ячейках должны быть равны (секторы диаграммы визуально равны).
• Получим выражения из формул ячеек, подставив вместо С1 -> x:
• Так как секторы диаграммы равны, то приравняем два из полученных выражений (например, С2 = В2):

Результат: 2

Детальный разбор можно посмотреть в видеоуроке решения данного 7 задания ЕГЭ по информатике:

Задан фрагмент электронной таблицы:

Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:C2 соответствовала рисунку:

✍ Решение:

• По диаграмме можно судить только о следующем: если она не перевернута, то значения в ячейках A2 и B2 должны быть равны, а значение ячейки C2 — в два раза больше каждой из них.
• Поскольку у нас неизвестны значения двух ячеек, то обозначим B1 за x, а C1 за y.
• Подставим неизвестные в формулы и получим:

Исходя из первого пункта, получаем:

Составим систему уравнений:

Первое уравнение нам дает x = 5y. Подставим это значение во второе уравнение:

Таким образом, x= 5 . А значения ячеек A2 = B2 = 4, C2 = 8. Т.е. изображение диаграммы действительно сходится с полученными значениями.

Результат: 5

Подробное решение смотрите на видео:

Дан фрагмент электронной таблицы в режиме отображения формул:

После копирования диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 была построена диаграмма (график) по значениям столбцов диапазона ячеек В2:Е6.

Значениям D2:D6 соответствует график:

Варианты:
1) А 2) Б 3) В 4) Г

✍ Решение:

• Копирование диапазона ячеек АЗ:ЕЗ в диапазон А4:Е6 буквально означает выделение диапазона АЗ:ЕЗ и протягивание маркера копирования до конца указанного блока ячеек.
• Поскольку нас интересует только столбец D, то посмотрим, что там за формула, и что с ней произойдет при копировании:

в ячейке D3 значение зависит от ячейки A3 и оно равно 2;

при копировании формулы столбец остается тот же (D), поэтому и в формуле буквы остаются теми же (D и A), а вот строки копируются вниз, т.е. цифры в формуле увеличиваются на единицу при движении вниз на каждую строку; соответственно, нас интересуют еще ячейки A4, A5, A6;

формулы ячеек A4, A5, A6 зависят от ячеек столбца B, поэтому рассмотрим получившиеся при копировании формулы столбцов A и B:

Теперь вычислим значения в этих столбцах:

Получаем точки по столбцу D: 1, -1, -1, -7, -15, что соответствует графику Г (ответ 4 )

Результат: 4

Разбор задания смотрите на видео:

Дан фрагмент электронной таблицы:


Какое целое число должно быть записано в ячейке C1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку? Известно, что все значения диапазона, по которым построена диаграмма, положительные.

✍ Решение задания 7:

• На изображенной диаграмме (если она преднамеренно не перевернута) секторы соответствуют указанному диапазону ячеек при движении по часовой стрелке с «севера на юг»: т.е. А2 — синий сектор, B2 — красный и т.п. Таким образом, делаем следующий вывод:
• Поскольку необходимо найти C1, и оно встречается в формулах, то примем его за x.
• Перепишем формулы согласно введенному обозначению:

Приравняем формулы в ячейках B2 и D2 (см. п.1) и получим:

Т.е. С1 = 11

Результат: 11

Источник